Hình học không gian lớp 11 đôi khi đặt ra những thách thức lớn đối với học sinh, đặc biệt là trong việc nắm vững kiến thức và vẽ hình chính xác. Dưới đây là một số mẹo học hình học không gian giúp học sinh tự tin hơn khi đối mặt với môn học này.

Nắm Vững Lý Thuyết với Sơ Đồ Tư Duy
Để vẽ hình không gian đúng và chính xác, việc đầu tiên là học thuộc lý thuyết. Học sinh cần nắm rõ các định nghĩa và định lý quan trọng của hình học không gian, như quan hệ song song, vuông góc trong không gian. Tuy nhiên, việc thuộc lý thuyết chỉ là bước đầu. Quan trọng hơn là biến kiến thức thành kỹ năng thông qua việc vận dụng vào bài tập.
Dạng Bài Tập Thông Thường:
- Tìm giao tuyến giữa hai mặt phẳng.
- Tìm giao điểm giữa đường thẳng và mặt phẳng.
- Chứng minh 3 điểm thẳng hàng.
- Chứng minh 3 đường thẳng đồng quy.
- Chứng minh đường thẳng song song với mặt phẳng.
Phương Pháp Thực Hiện:
Sử dụng phương pháp 1 và 2 để tìm giao tuyến giữa hai mặt phẳng.
Áp dụng phương pháp tổng quát để tìm giao điểm đường thẳng và mặt phẳng.
-
Dạng 1: Tìm giao tuyến giữa hai mặt phẳng ( P ) và ( Q )
Phương pháp 1: Tìm 2 điểm chung của 2 mặt phẳng đó.
– Điểm thứ nhất thường thì các bạn dễ nhìn ra
– Điểm thứ hai là giao của hai đường thẳng nằm trong hai mặt phẳng ( P ) và ( Q ) không đi qua điểm chung thứ nhất.
Phương pháp 2: Nếu mặt phẳng ( P ) và ( Q ) có chứa hai đường thẳng song song thì chỉ cần tìm một điểm chung. Khi đó giao tuyến của hai mặt phẳng sẽ là đường thẳng đi qua điểm chung và song song với hai đường thẳng này.
Dạng 2: Tìm giao điểm của đường thẳng d và mặt phẳng ( α ).
Phương pháp tổng quát:
Trường hợp 1: Trong mặt phẳng (α) có sẵn đường thẳng d’ cắt d tại H. Ta có ngay d ∩ (α) = H.
Trường hợp 2: Trong mặt phẳng không có sẵn d1 cắt d. Khi đó ta làm bước sau:
– Chọn mặt phụ (β) chứa d và (β) cắt (α) theo giao tuyến d’. Khi đó: H = d’ ∩ d
Dạng 3: Chứng minh 3 điểm cùng nằm trên một đường thẳng
Phương pháp: Chứng minh 3 điểm A, B, C thằng hàng.
– Ta chứng minh A, B, C cùng thuộc hai mặt phẳng phân biệt
Dạng 4: chứng minh 3 đường thẳng đồng quy
Phương pháp: Chứng minh 3 đường thẳng d1, d2, d3 đồng quy.
Phương pháp 1: Chứng minh giao của hai đường thẳng bất kỳ là điểm chung của hai mặt phẳng mà giao tuyến là đường thẳng thứ ba. Cụ thể:
– Tìm giao điểm của d1 X d2 = H.
– Tìm 2 mặt phẳng (α) và (β) chứa điểm H sao cho: (α) ∩ (β) = d3
Phương pháp 2: Ta chứng minh d1, d2, d3 không đồng phẳng và cắt nhau từng đôi một.
Dạng 5: Chứng minh đường thẳng d song song với mặt phẳng (α).
Phương pháp 1: Chứng minh d // (α) ta chứng minh d // d’, với d’ ⊂ (α).
Phương pháp 2: Chứng minh đường thẳng d nằm trong mặt phẳng khác và song song với mặt phẳng đã cho
– Chứng minh d ⊂ (β). Sao cho: (α) // (β).
Tưởng Tượng và Vẽ Hình Chính Xác
Một yếu tố quan trọng khác là khả năng tưởng tượng và vẽ hình chính xác. Trước khi bắt tay vào vẽ, học sinh nên đọc đề bài kỹ và tưởng tượng mặt phẳng nào có thể nhìn thấy. Sử dụng bút chì để vẽ trước, giúp tránh sai sót trước khi chuyển sang bút mực.
Luyện Tập Thật Nhiều
Châm ngôn \”Cần cù bù thông minh\” là quan trọng trong việc học hình không gian. Học sinh càng kiên trì và luyện tập nhiều, họ sẽ càng vận dụng kiến thức lý thuyết tốt hơn. Đặc biệt, khi mới tiếp xúc với hình học không gian, việc tập vẽ hình từ nhiều góc nhìn khác nhau là rất quan trọng.
Đầu Tư Thời Gian và Tham Khảo Sách Hình Học Không Gian 11
Sách giáo khoa và sách bài tập là nguồn kiến thức cơ bản, nhưng để hiểu sâu và áp dụng linh hoạt, học sinh cần đầu tư thêm thời gian vào việc tham khảo sách hướng dẫn. Ngoài ra, có thể tìm kiếm trên mạng để đọc thêm về những mẹo vẽ hình sáng tạo và khoa học.
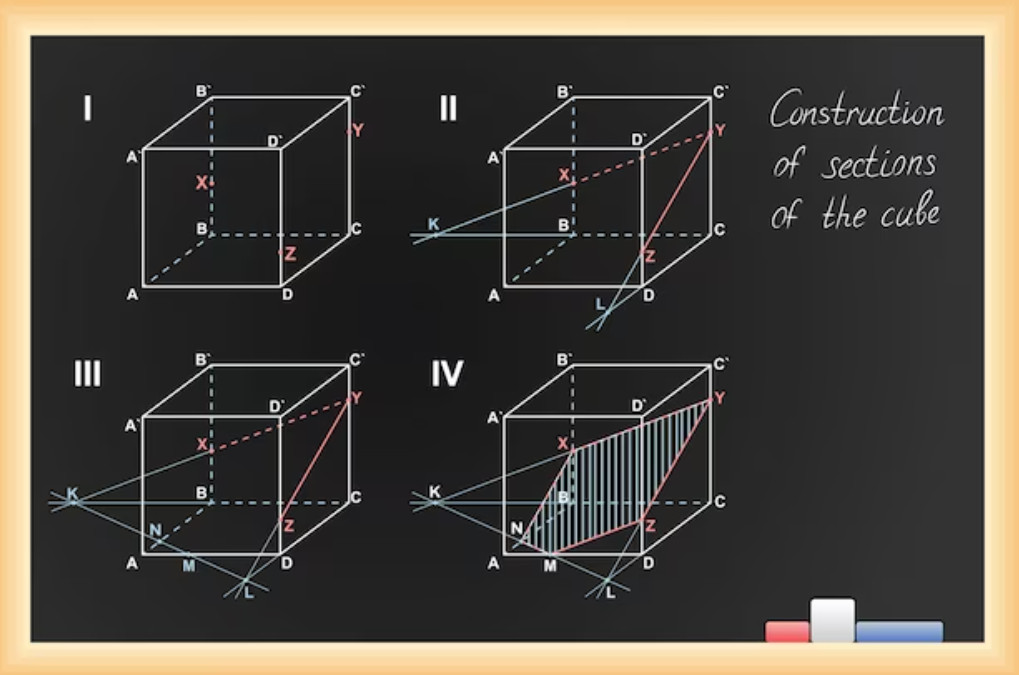
Kết Luận
Với những mẹo học này, học sinh không chỉ có khả năng nắm vững hình học không gian mà còn có thể áp dụng kiến thức vào thực tế một cách hiệu quả. Hãy kiên trì và sẵn sàng học hỏi từ những thách thức, từ đó họ sẽ đạt được kết quả tốt nhất trong hành trình học tập của mình.
Tham Khảo: giasusupham.com.vn
Xem thêm:











